By guest contributor Audrey Borowski

Gottfried Wilhelm Leibniz, painted by Christoph Bernhard Francke
According to the philosopher of science Alexandre Koyré, the early modern period marked the passage ‘from the world of more-or-less to the universe of precision’. Not all thinkers greeted the mathematization of epistemology with the same enthusiasm: for the German philosopher Martin Heidegger, this marked a watershed moment when modern nihilism had taken root in the shape of the reduction of the world to calculation and recently culminated with the emergence of cybernetics. One of the main culprits of this trend was none other than the German mathematician and polymath Gottfried Leibniz (1646-1716), who in the late seventeenth century invented the calculus and envisaged a binary mathematical system. Crucially, Leibniz had concerned himself with the formalization and the mechanization of the thought process either through the invention of actual calculating machines or the introduction of a universal symbolic language – his so-called ‘Universal characteristic’– which relied purely on logical operations. Ideally, this would form the basis for a general science (mathesis universalis). According to this scheme, all disputes would be ended by the simple imperative ‘Gentlemen, let us calculate!’
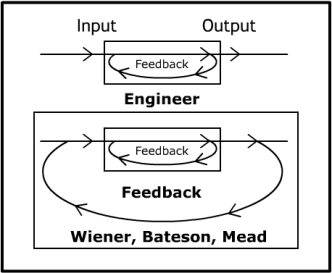
A graphic representation of second-order cybernetics by Mark Côté
For having mechanized reasoning, cyberneticist Norbert Wiener touted Leibniz as a ‘patron saint for cybernetics’ (Wiener 1965, p. 12) in the ‘Introduction’ to his 1948 seminal work Cybernetics or Control and Communication in the Animal and the Machine. In it, he settled on the term ‘kybernetes’, the ‘steersman’ to describe a novel type of automatic and self-correcting reasoning which consisted in the deployment of mathematics, notably via a feedback mechanism, towards the domestication of contingency and unpredictability. Cybernetics does not ‘drive toward the ultimate truth or solution, but is geared toward narrowing the field of approximations for better technical results by minimizing on entropy––but never being able to produce a system that would be at an entropy of zero…. In all of this, [it] is dealing with data as part of its feedback mechanism for increasing the probability of a successful event in the future (or in avoiding unwanted events).’
Cybernetic applications are ubiquitous today from anti-aircraft systems to cryptography; an anti-aircraft system, for instance, receives input data on a moving target and delivers the navigation of bullet to the target as output after a computing process. Cybernetics’ aim is first and foremost practical and its method probabilistic: through the constant refining of the precision of a prediction, it helps steer action through the selection between probabilities. Under those conditions, a constant process of becoming is subordinated to a weak form of determinism; real infinite complexity is deferred in favour of logical symbolism and ‘disorganization’, that ‘arch-enemy’ endemic to intense mutability as Nobert Wiener put it, gives way to ontological prediction.
In his works The Taming of Chance and The Emergence of Probability Ian Hacking traced the emergence of probabilistic thinking away from deterministic causation. In fact and against commonly-held positivist narratives of the triumph of objective rationality, historians of mathematics generally acknowledge that the seventeenth century witnessed the birth of both probability theory and modern probabilism perhaps most famously epitomized by Pascal’s Wager. With the emergence of contingency, the question of its conceptualization became all the more pressing.
Perhaps no thinker was more aware of this imperative than Leibniz. Leibniz is often portrayed as an arch-rationalist and yet he did not view pure deduction as sufficient for reasoning; the ‘statics’ inherent to his characteristic (Leibniz, 1677) were simply ill-suited to a constantly evolving practical reality. Finite calculation needed to be complemented by probabilistic reasoning (1975, p. 135) which would better embrace the infinite complexity and evolving nature of reality. Although the author of a conjectural history of the world, The Protogaea, Leibniz did not merely conjecture about the past, but also sought to come to grips with the future and the state of mutability of the world. To this end, he pioneered the collection of statistical data and probabilistic reasoning especially with regards to the advancement of the modern state or the public good (Taming of Chance, 18). Leibniz had pored over degrees of probability as early as his 1665 law degree essay De conditionibus and the ability to transmute uncertainty into (approximate) certainty in conditions of constant mutability remained a lifelong preoccupation. More specifically, he set out to meet the challenge of mutability with what appears as a cybernetic solution.
An example of Leibniz’s diagrammatic reasoning
In a series of lesser-known texts Leibniz explored the limits and potentially dangerous ramifications of finite cognition, and the necessity for flexible and recursive reasoning. In 1693 Leibniz penned The Horizon of the Human Doctrine, a thought experiment which he subtitled: ‘Meditation on the number of all possible truths and falsities, enunciable by humanity such as we know it to be; and on the number of feasible books. Wherein it is demonstrated that these numbers are finite, and that it is possible to write, and easy to conceive, a much greater number. To show the limits of the human spirit [l’esprit humain], and to know the extent to these limits’. Building on his enduring fascination with combinatorial logic that had begun as a teenager in 1666 with his De Arte Combinatoria and had culminated ten years later with his famous ‘Universal Characteristic’, he set out to ‘show the limits of the human spirit, and to know the extent to these limits’. Following in the footsteps of Clavius, Mersenne and Guldin, Leibniz reached the conclusion that, through the combination of all 23 letters of the alphabet, it would be possible to calculate the number of all possible truths. Considering their prodigious, albeit ultimately finite number, there would inevitably come a point in time when all possible variations would have been exhausted and the ‘horizon’ of human doctrine would be reached and when nothing could be said or written that had not been expressed before (nihil dici, quod non dictum sit prius) (p. 52). The exhaustion of all possibilities would give way to repetition.
In his two later treatments on the theme of apokatastasis, or ‘universal restitution’, Leibniz took this reasoning one step further by exploring the possible ramifications of the limits of human utterability for reality. In them, he extended the rule of correspondence between possible words to actual historical events. For instance, since ‘facts supply the matter for discourse’ (p. 57), it would seem, by virtue of this logic, that events themselves must eventually exhaust all possible combinations. Accordingly, all possible public, as well as individual histories, would be exhausted in a number of years, inevitably incurring a recurrence of events, whereby the exact same circumstances would repeat themselves, returning ‘such as it was before.’ (p.65):
‘[S]uppose that one day nothing is said that had not already been said before; then there must also be a time when the same events reoccur and when nothing happens which did not happen before, since events provide the matter for words.’
In a passage he later decided to omit, Leibniz even muses about his own return, writing once again the same letters to the same friends.
Now from this it follows: if the human race endured long enough in its current state, there would be a time when the same life of certain individuals would return in detail through the very same circumstances. I myself, for example, would be living in a city called Hanover situated on the river Leine, occupied with the history of Brunswick, and writing letters to the same friends with the same meaning. [Fi 64]
Leibniz contemplated the doctrine of Eternal Return, but it was incompatible with his metaphysical understanding of the world. Ultimately, he reasserted the primacy of the infinite complexity of the world over finite combinatorics. Beneath the superficial similarity of events – and thus of description- lay a trove of infinite differences which superseded any finite number of combinations: paradoxically, ‘even if a previous century returns with respect to sensible things or which can be described by books, it will not return completely in all respects: since there will always be differences although imperceptible and such that could not be sufficiently described in any book however long it is.’. [Fi 72]’ Any repetition of event was thus only apparent; each part of matter contained the ‘world of an infinity of creatures’ which ensured that truths of fact ‘could be diversified to infinity’ (p. 77).
To this epistemological quandary Leibniz opposed a ‘cybernetic’ solution whereby the analysis of the infinite ‘detail’ of contingent reality would open up a field of constant epistemological renewal which lay beyond finite combinatorial language, raising the prospect of an ‘infinite progress in knowledge’ for those spirits ‘in search of truth.’ (p. 59) The finite number of truths expressible by humans at one particular moment in time would be continuously updated to adapt itself to the mutability and progress of the contingent world. ‘Sensible truths’ could ‘always supply new material and new items of knowledge, i.e. in theorems increasing in length’ in this manner permitting knowledge to approach reality asymptotically. In this manner, the theoretical limits which had been placed upon human knowledge could be indefinitely postponed, in the process allowing for incrementally greater understanding of nature through constant refinement.
Leibniz thus set forth an ingenious solution in the shape of a constantly updated finitude which would espouse the perpetually evolving infinity of concrete reality. By adopting what may be termed a ‘cybernetic’ solution avant la lettre, he offered a model, albeit linear and continuous, which could help reconcile determinism and probabilism, finite computation and infinite reality and freedom and predictability. Probabilism here served to induce and sustain a weak form of determinism, one which, in keeping with the nature of contingency itself as defined by Leibniz, ‘inclined’ rather than ‘necessitated’.
Audrey Borowski is a historian of ideas at the University of Oxford.


February 5, 2018 at 9:45 am
This is a most stimulating article!